
Zastanawiasz się co to jest kwartyl? Nie wiesz jak obliczyć IQR? Pokaże Ci tutaj w prosty sposób o co chodzi.
Podstawy statystyki, czyli co to jest kwartyl
Aby odpowiedzieć na pytanie, co to jest kwartyl najlepiej przypomnieć sobie medianę. Mediana jest bowiem środkową wartością uporządkowanych liczb. Jeżeli liczba elementów (liczba liczb mówiąc bardzo dosadnie 😀 ) jest parzysta, to bierzemy średnią z dwóch środkowych.
OK. I teraz jak mamy te uporządkowane liczby, z medianą w środku, to możemy sobie wyobrazić, że dzielimy ten sam zbiór po prostu na 4 części.
Weźmy taki zestaw liczb:
1 3 3 5 8 8 8 9
Mediana leży po środku – między 5 a 8, czyli wynosi 6,5. Swoją drogą to właśnie drugi kwartyl.
A jak obliczyć pierwszy kwartyl? Albo trzeci?

Obrazek powyżej to pokazuje. Mediana dzieli nam zbiór dokładnie na pół. W ten sposób widać, że:
- w górnym przykładzie Q1 (czyli pierwszy kwartyl) wynosi 3, a Q3 (trzeci kwartyl) wynosi 8
- w dolnym przykładzie Q1 =3, a Q3 = 8,5
Jeżeli wolisz raczej obejrzeć filmik o tym, co to jest kwartyl zamiast czytać – to odsyłam do mojego YouTube.
To ważne w środku, czyli jak obliczyć IQR
OK, wiesz już co to jest kwartyl, więc teraz pytanie jak obliczyć IQR.
Co to w IQR? Z angielskiego interquartile range (czyli w skrócie właśnie IQR) to po prostu różnica między trzecim kwartylem a pierwszym.
Innymi słowy wzór na IQR to:
IQR = Q3 – Q1
W ten sposób uzyskujemy 50% naszych obserwacji – tych położonych najbardziej „w środku”. Stąd też im większy IQR, tym większy „środek”, a co za tym idzie większe zróżnicowanie.
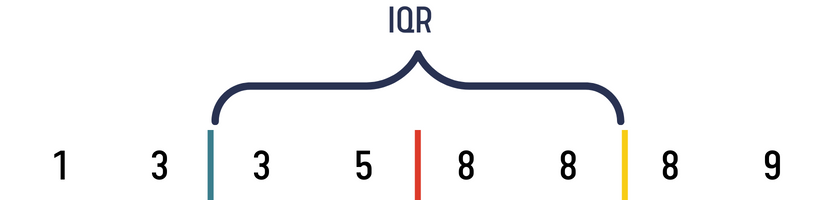
Na obrazku powyżej IQR wynosi 5 (ponieważ 8 – 3 = 5).
Po polsku IQR to rozstęp międzykwartylowy, przedział międzykwartylowy albo rozstęp kwartylny, ale ja zdecydowanie wolę angielską nazwę.
Podsumowanie
- Co to jest kwartyl? W statystyce kwartyl dzieli liczbę punktów danych na cztery mniej więcej równe części. Aby obliczyć kwartyle, dane muszą być uporządkowane od najmniejszego do największego.
- Jak obliczyć IQR? Po prostu policzyć różnicę między kwartylem pierwszym a trzecim.
A może pora odświeżyć średnią ważoną? Ewentualnie, jeśli takie banały nie są dla Ciebie, to może odchylenie standardowe?
To tyle w tym temacie. Analizujcie w pokoju!
Podobał Ci się ten artykuł 🙂?
Podziel się nim w Social Mediach 📱
>>> udostępnij go na LinkedIn i pokaż, że codziennie uczysz się czegoś nowego
>>> wrzuć go na Facebooka, to się może przydać któremuś z Twoich znajomych
>>> Przypnij sobie tą stronkę to zakładek, może się przydać w przyszłości
Wolisz oglądać 📺 niż czytać – nie ma problemu
>>> Obserwuj i oglądaj KajoData na YouTube
Inne ciekawe artykuły:



